Vyskúšajte si online editor rovníc.
Pripravil som jednoduchý návod.
Editor rovníc nájdete na stránke http://www.codecogs.com/latex/eqneditor.php.
Archívy kategórie: Pre učiteľov
Obor hodnôt
Úloha. Aké hodnoty môže nadobúdať výraz
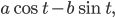
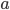 ,
, 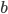 sú kladné konštanty a
sú kladné konštanty a 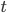 je ľubovoľné reálne číslo?
je ľubovoľné reálne číslo?Riešenie. Stačí si uvedomiť, že existuje taký uhol
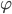 , že platí
, že platí 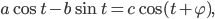
 je vhodná konštanta. Naozaj,
je vhodná konštanta. Naozaj, 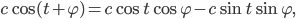
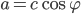 a
a 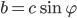 . Potom
. Potom 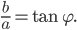
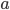 a
a 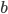 . Potom prepona tohto trojuholníka má dĺžku
. Potom prepona tohto trojuholníka má dĺžku 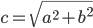 . Pretože kosínus môže nadobúdať ľubovoľnú hodnotu z intervalu
. Pretože kosínus môže nadobúdať ľubovoľnú hodnotu z intervalu 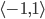 , výraz
, výraz 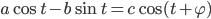
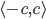 .
.
Súčet radu: príklad
The William Lowell Putnam Mathematical Competition 1988
Problem B-4. Dokážte, že ak 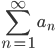 je konvergentný číselný rad s kladnými členmi, potom aj rad
je konvergentný číselný rad s kladnými členmi, potom aj rad 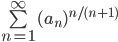 je konvergentný.
je konvergentný.
Riešenie: Využijeme nerovnosť medzi aritmetickým a geometrickým priemerom.
\begin{align}
a_n^{\frac{n}{n+1}}&=\sqrt[n+1]{\frac1{n+3}\cdot(n+3)a_n\cdot a_n^{n-1}}\leq\\ &\leq\frac{\frac1{n+3}+(n+3)a_n+(n-1)a_n}{n+1}=\\ &=\frac1{(n+1)(n+3)}+2a_n.
\end{align}
Pozrite si aj ďalšie riešenia.
Učíme sa písať matematické výrazy
V texte: 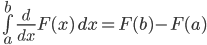
Na samostatnom riadku:
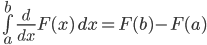
Ak chcete vidieť syntax, položte kurzor myši na matematický výraz a použite pravé tlačítko myši.