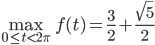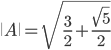Úloha. Vypočítajte operátorovú normu matice 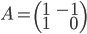 .
.
Riešenie. Pre 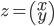 také, že
také, že 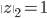 , platí
, platí 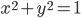 . Položme
. Položme 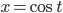 a
a 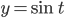 . Potom
. Potom
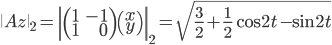
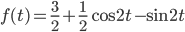
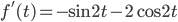

V pravouhlom trojuholníku s odvesnami dĺžky 1 a 2 máme uhol
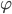 , ktorého tangens je rovný číslu 2.
, ktorého tangens je rovný číslu 2.Prepona tohto trojuholníka má dĺžku
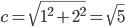
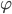 platí
platí\begin{align} \sin\varphi&=\frac{2}{\sqrt{5}}\\ \cos\varphi&=\frac{1}{\sqrt{5}}\end{align}
Potom \begin{align}f(t)&=\frac{3}{2}+\frac{\sqrt{5}}{2}\left(\frac{1}{\sqrt{5}}\cos2t-\frac{2}{\sqrt{5}}\sin2t\right)=\\ &=\frac{3}{2}+\frac{\sqrt{5}}{2}\left(\cos\varphi\cos2t-\sin\varphi\sin2t\right)=\\ &=\frac{3}{2}+\frac{\sqrt{5}}{2}\cos(\varphi+2t)\end{align} Odtiaľ