Úloha. Aké hodnoty môže nadobúdať výraz
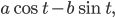
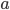 ,
, 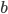 sú kladné konštanty a
sú kladné konštanty a 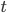 je ľubovoľné reálne číslo?
je ľubovoľné reálne číslo?Riešenie. Stačí si uvedomiť, že existuje taký uhol
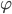 , že platí
, že platí 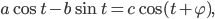
 je vhodná konštanta. Naozaj,
je vhodná konštanta. Naozaj, 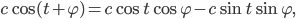
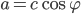 a
a 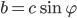 . Potom
. Potom 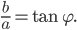
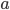 a
a 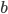 . Potom prepona tohto trojuholníka má dĺžku
. Potom prepona tohto trojuholníka má dĺžku 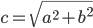 . Pretože kosínus môže nadobúdať ľubovoľnú hodnotu z intervalu
. Pretože kosínus môže nadobúdať ľubovoľnú hodnotu z intervalu 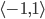 , výraz
, výraz 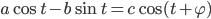
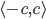 .
.