V sekcii Matematická analýza IV bol pridaný materiál o vzájomnom vzťahu medzi nevlastným Riemannovým integrálom a Lebesgueovým integrálom na reálnej osi.
Veta. Nech funkcia 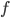 je integrovateľná na intervale
je integrovateľná na intervale 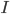 (ohraničenom alebo neohraničenom) v nevlastnom Riemannovom zmysle spolu aj s funkciou
(ohraničenom alebo neohraničenom) v nevlastnom Riemannovom zmysle spolu aj s funkciou 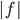 . Potom
. Potom 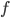 je Lebesgueovsky integrovateľná na
je Lebesgueovsky integrovateľná na 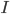 a jej nevlastný Riemannov integrál sa rovná jej Lebesgueovmu integrálu. Môžete použiť aj priamy link.
a jej nevlastný Riemannov integrál sa rovná jej Lebesgueovmu integrálu. Môžete použiť aj priamy link.